358
476
всего разделов:
активных пользователей:
30 мартра 2005
Форумы снова функционируют.
21 декабря 2004
Видимо в связи с обнаруженными дырами в phpBB, форум был взломан, а через него взломано и всё остальное содержимое ceemat.ru. Всё кроме форума восстановлено, ведется дискуссия по поводу его сохранения.
Приносим извинения за неудобства.
29 сентября 2004
Форум обновился до версии 2.0.10
15 мая 2004
Новый раздел: "Программирование"
16 апреля 2004 года
Задачи Ярославского турнира математических боев — 124 задачи с решениями.
29 марта 2004
Таллинская викторина: занимательные вопросы и задачи для увлеченных химией.
Осень 2002 года (25)
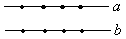
Даны две параллельные прямые. На каждой прямой отмечено по четыре точки. Сколько можно построить треугольников с вершинами в этих точках? |
Ответ: Пусть a и b — прямые, содержащие 4 точки.
Чтобы составить треугольник, нужно выбрать три вершины. При этом одна вершина находится на одной прямой, а две другие — на второй, или наоборот (три вершины на одной прямой находиться не могут). Рассмотрим эти случаи. На прямой a находятся две вершины, на прямой b — одна. Найдем, сколькими способами можно выбрать на прямой a пару точек различного положения. Первую точку можно выбрать 4 способами и на каждый из этих способов — 3 способа выбрать вторую точку, то есть всего 3 × 4 = 12 способов. Но каждый способ повторился дважды (например, сначала точку X выбрали первой, а точку Y — второй, а потом наоборот), значит выбрать пару точек можно 6 способами. На каждый из этих шести способов есть 4 способа для выбора третьей вершины на прямой b, то есть всего 24 треугольника. Если на прямой b находятся две вершины, на прямой a — одна, то получим так же 24 треугольника. Таким образом, всего различных треугольников 24 × 2 = 48. |
9 Марта 2004 20:16 Раздел каталога :: Ссылка на задачу
|