358
471
всего разделов:
активных пользователей:
30 мартра 2005
Форумы снова функционируют.
21 декабря 2004
Видимо в связи с обнаруженными дырами в phpBB, форум был взломан, а через него взломано и всё остальное содержимое ceemat.ru. Всё кроме форума восстановлено, ведется дискуссия по поводу его сохранения.
Приносим извинения за неудобства.
29 сентября 2004
Форум обновился до версии 2.0.10
15 мая 2004
Новый раздел: "Программирование"
16 апреля 2004 года
Задачи Ярославского турнира математических боев — 124 задачи с решениями.
29 марта 2004
Таллинская викторина: занимательные вопросы и задачи для увлеченных химией.
Математическая регата (12)
Пусть A и B — фиксированные точки на плоскости. Укажите геометрическое место точек M этой плоскости, для которых угол ABM — средний по величине в треугольнике AMB. |
Если A и B — фиксированные точки на плоскости, то AMB является треугольником тогда и только тогда, когда точка М не лежит на прямой АВ. Для того чтобы ÐАВМ был средним по величине углом в этом треугольнике необходимо и достаточно, чтобы выполнялось одно из неравенств: BM > АМ > AB или AB > АМ > BМ. В первом случае, условие АМ > AB равносильно тому, что М лежит вне круга с центром A и радиусом АВ, а условие BМ > AМ равносильно тому, что точки A и М лежат в одной полуплоскости относительно серединного перпендикуляра к отрезку АВ. Во втором случае, условие AB > AM равносильно тому, что точка M лежит внутри круга с центром A и радиусом АВ, а условие AM > BM равносильно тому, что точки B и M лежат в одной полуплоскости относительно серединного перпендикуляра к отрезку АВ. |
1 Марта 2004 22:13 Раздел каталога :: Ссылка на задачу
|
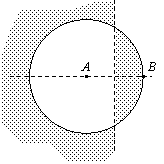Ответ: показано на рисунке.