358
471
всего разделов:
активных пользователей:
30 мартра 2005
Форумы снова функционируют.
21 декабря 2004
Видимо в связи с обнаруженными дырами в phpBB, форум был взломан, а через него взломано и всё остальное содержимое ceemat.ru. Всё кроме форума восстановлено, ведется дискуссия по поводу его сохранения.
Приносим извинения за неудобства.
29 сентября 2004
Форум обновился до версии 2.0.10
15 мая 2004
Новый раздел: "Программирование"
16 апреля 2004 года
Задачи Ярославского турнира математических боев — 124 задачи с решениями.
29 марта 2004
Таллинская викторина: занимательные вопросы и задачи для увлеченных химией.
Математическая регата (12)
Известно, что a2 + b2 = 1 и с2 + d2 = 1. Может ли оказаться, что ac + bd > 1? |
Ответ: нет. Решение 1. Предположим, что ac + bd > 1. Умножим обе части этого неравенства на –2 и сложим получившееся с данными равенствами. Получим, что a2 + b2 + с2 + d2 – 2ac – 2bd < 0 Û (a – c)2 + (b – d)2 < 0 — противоречие. Решение 2.
|
1 Марта 2004 22:11 Раздел каталога :: Ссылка на задачу
|
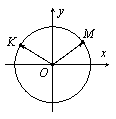Рассмотрим окружность с центром (0; 0) и радиусом 1 в декартовой системе координат. Пусть М (a; b), K (c; d), тогда из условия следует, что эти точки лежат на окружности (показано на рисунке).
Вектора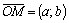 
, 
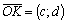— единичные. Следовательно,