358
476
всего разделов:
активных пользователей:
30 мартра 2005
Форумы снова функционируют.
21 декабря 2004
Видимо в связи с обнаруженными дырами в phpBB, форум был взломан, а через него взломано и всё остальное содержимое ceemat.ru. Всё кроме форума восстановлено, ведется дискуссия по поводу его сохранения.
Приносим извинения за неудобства.
29 сентября 2004
Форум обновился до версии 2.0.10
15 мая 2004
Новый раздел: "Программирование"
16 апреля 2004 года
Задачи Ярославского турнира математических боев — 124 задачи с решениями.
29 марта 2004
Таллинская викторина: занимательные вопросы и задачи для увлеченных химией.
Математическая регата (12)
Длины сторон треугольника — последовательные натуральные числа. Найдите их, если известно, что одна из медиан треугольника перпендикулярна одной из его биссектрис. |
Ответ: 2; 3; 4. Отметим, что перпендикулярные медиана и биссектриса не могут выходить из одной вершины, так как тогда угол при этой вершине окажется больше, чем 180°.
Несложно, но обязательно убедиться, что для треугольника со сторонами 2, 3 и 4 условие перпендикулярности медианы и биссектрисы выполняется. |
1 Марта 2004 22:09 Раздел каталога :: Ссылка на задачу
|
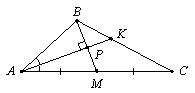 Пусть АВС — данный треугольник, в котором медиана BМ перпендикулярна биссектрисе АK и они пересекаются в точке P (показано на рисунке). Тогда AP — биссектриса и высота треугольника АВМ, следовательно, АВ = AM = AC : 2. Так как длины сторон треугольника АВС — последовательные натуральные числа, то осталось проверить только два варианта: AB = 1, AC = 2 или AB = 2, AC = 4. В обоих случаях остается принять, что ВС = 3, но первый вариант невозможен, так как не выполняется неравенство треугольника.
Пусть АВС — данный треугольник, в котором медиана BМ перпендикулярна биссектрисе АK и они пересекаются в точке P (показано на рисунке). Тогда AP — биссектриса и высота треугольника АВМ, следовательно, АВ = AM = AC : 2. Так как длины сторон треугольника АВС — последовательные натуральные числа, то осталось проверить только два варианта: AB = 1, AC = 2 или AB = 2, AC = 4. В обоих случаях остается принять, что ВС = 3, но первый вариант невозможен, так как не выполняется неравенство треугольника.