358
475
всего разделов:
активных пользователей:
30 мартра 2005
Форумы снова функционируют.
21 декабря 2004
Видимо в связи с обнаруженными дырами в phpBB, форум был взломан, а через него взломано и всё остальное содержимое ceemat.ru. Всё кроме форума восстановлено, ведется дискуссия по поводу его сохранения.
Приносим извинения за неудобства.
29 сентября 2004
Форум обновился до версии 2.0.10
15 мая 2004
Новый раздел: "Программирование"
16 апреля 2004 года
Задачи Ярославского турнира математических боев — 124 задачи с решениями.
29 марта 2004
Таллинская викторина: занимательные вопросы и задачи для увлеченных химией.
Математическая регата (12)
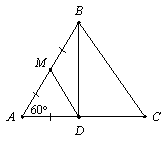
В треугольнике АВС: AB = 2, ÐA = 60°, ÐB = 70°. На стороне АС взята такая точка D, что AD = 1. Найдите углы треугольника DBC. |
Ответ: 90°; 50°; 40°. Пусть АВС — данный треугольник (см. рисунки), тогда ÐDCB = 180° – (ÐA + ÐB) = 50°.
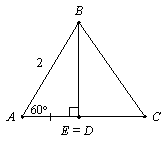
Первый способ. В треугольнике ABD проведем медиану DM, тогда AM = AD = 1. Так как ÐMAD = 60°, то DMAD – равносторонний. Следовательно, MD = AM = MB, то есть, DABD — прямоугольный с прямым углом В. Значит, ÐBDC = 90°; ÐDBC = 40°. Второй способ. В треугольнике ABC проведем высоту BE, тогда ÐABE = 30°, значит, катет AE прямоугольного треугольника ABE равен половине гипотенузы AB. Следовательно, AE = 1, то есть, точка E совпадает с данной точкой D. Значит, ÐBDC = 90°, ÐDBC = 40°. |
Замечание. Длину BD также можно вычислить из треугольника ABD по теореме косинусов ( |
1 Марта 2004 22:05 Раздел каталога :: Ссылка на задачу
|
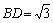 ) и, используя теорему, обратную теореме Пифагора, доказать, что угол ADB — прямой.
) и, используя теорему, обратную теореме Пифагора, доказать, что угол ADB — прямой.