358
475
всего разделов:
активных пользователей:
30 мартра 2005
Форумы снова функционируют.
21 декабря 2004
Видимо в связи с обнаруженными дырами в phpBB, форум был взломан, а через него взломано и всё остальное содержимое ceemat.ru. Всё кроме форума восстановлено, ведется дискуссия по поводу его сохранения.
Приносим извинения за неудобства.
29 сентября 2004
Форум обновился до версии 2.0.10
15 мая 2004
Новый раздел: "Программирование"
16 апреля 2004 года
Задачи Ярославского турнира математических боев — 124 задачи с решениями.
29 марта 2004
Таллинская викторина: занимательные вопросы и задачи для увлеченных химией.
Вторая лига (8)
Натуральные числа от 1 до 22 записаны в такой последовательности a1, a2, …, a22, что
Чему равна сумма |
Ответ: 121. Какое наибольшее значение может принимать сумма
Каждое число ai (1 £ i £ 22) появляется в сумме дважды. При раскрытии знака абсолютной величины одно из чисел “выйдет” со знаком “плюс”, а второе — со знаком “минус”. Значит, наибольшего значения эта сумма достигнет только в том случае, когда каждое из наибольших чисел (от 12 до 22) два раза войдет со знаком “плюс”, а каждое из наименьших чисел (от 1 до 11) два раза войдет со знаком “минус”. Тогда эта сумма будет равна 2 × (12 + 13 + … + 22 - 1 - 2 - … - 11) = 242. Так как, по условию, эта сумма равна 242, то имеет место именно такое распределение, то есть все числа с четными (или нечетными) индексами — наибольшие, а с нечетными (или, наоборот, четными) индексами — наименьшие. Тогда значение суммы, которое требуется найти, — разность между суммой наибольших и наименьших чисел, то есть 12 + 13 + … + 22 - 1 - 2 - … - 11 = 121. |
Автор: В. Произволов. |
28 Февраля 2004 22:54 Раздел каталога :: Ссылка на задачу
|
 .
. ?
? 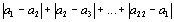 ?
?