358
476
всего разделов:
активных пользователей:
30 мартра 2005
Форумы снова функционируют.
21 декабря 2004
Видимо в связи с обнаруженными дырами в phpBB, форум был взломан, а через него взломано и всё остальное содержимое ceemat.ru. Всё кроме форума восстановлено, ведется дискуссия по поводу его сохранения.
Приносим извинения за неудобства.
29 сентября 2004
Форум обновился до версии 2.0.10
15 мая 2004
Новый раздел: "Программирование"
16 апреля 2004 года
Задачи Ярославского турнира математических боев — 124 задачи с решениями.
29 марта 2004
Таллинская викторина: занимательные вопросы и задачи для увлеченных химией.
Вторая лига (8)
Хоккейный чемпионат проводится по следующим правилам. Каждая команда играет с каждой из остальных ровно один раз. За победу дается 2 очка, за ничью — 1, за поражение — 0. Если по итогам чемпионата две команды набрали одинаковое число очков, более высокое место достается команде, у которой больше разница между числом забитых и пропущенных шайб. В результате: чемпион набрал 7 очков, серебряный призер — 5, бронзовый — 3. Сколько очков набрала команда, занявшая последнее место? |
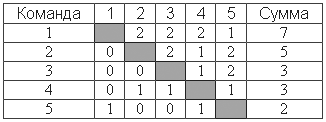
Ответ: два очка. Пусть в турнире участвовало n команд. Тогда было разыграно п × (п - 1) очков. Последние (п - 3) команды (то есть все, кроме занявших первые 3 места) набрали не более чем по 3 очка каждая. Поэтому n × (n - 1) £ 7 + 5 + 3 + 3 × (n - 3), то есть n2 - 4n - 6 £ 0, откуда n £ 5. Допустим, n £ 4. Тогда всего в чемпионате было разыграно не больше 4 × 3 = 12 очков, тогда как только первые трое набрали 7 + 5 + 3 = 15 очков, противоречие. Поэтому п = 5, то есть всего было 5 команд, которые разыграли между собой 5 × 4 = 20 очков. Пусть четвертая (по итогам чемпионата) команда набрала x очков, а последняя — y очков. Тогда у £ х £ 3, и общее число разыгранных очков: 7 + 5 + 3 + + х + у = 20, откуда х + у = 5. Так как у £ x £ 3, то x = 3, у = 2. Значит, команда, занявшая последнее место, набрала 2 очка. Такой турнир возможен (на пересечении строк и столбцов показано число очков, набранных командой).
|
Авторы: Е. Барабанов, И. Воронович. |
28 Февраля 2004 22:41 Раздел каталога :: Ссылка на задачу
|