358
475
всего разделов:
активных пользователей:
30 мартра 2005
Форумы снова функционируют.
21 декабря 2004
Видимо в связи с обнаруженными дырами в phpBB, форум был взломан, а через него взломано и всё остальное содержимое ceemat.ru. Всё кроме форума восстановлено, ведется дискуссия по поводу его сохранения.
Приносим извинения за неудобства.
29 сентября 2004
Форум обновился до версии 2.0.10
15 мая 2004
Новый раздел: "Программирование"
16 апреля 2004 года
Задачи Ярославского турнира математических боев — 124 задачи с решениями.
29 марта 2004
Таллинская викторина: занимательные вопросы и задачи для увлеченных химией.
Высшая лига и лига 9 классов (8)
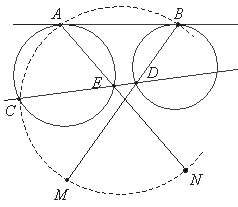
Через точку пересечения внешних касательных к двум окружностям проведена секущая CD и касательная AB, как показано на рисунке. Лучи AE и BD пересекают окружность, проведенную через точки A, B и C, в точках M и N. Докажите, что прямые CD и MN параллельны.
|
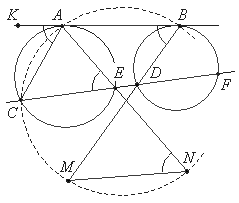
Углы MNA и MBA равны как вписанные, опирающиеся на одну дугу окружности (ACM). Прямые BD и AC параллельны, так как переходят друг в друга при гомотетии, переводящей окружность (ACE) в окружность (BDF). Значит, ÐMBA = ÐCAK. Так как AB — касательная к окружности ACE, то ÐCEA = ÐCAK. Получаем (показано на рисунке), что ÐMNA = ÐCEA, откуда следует параллельность прямых MN и CD.
|
Автор: Д. Калинин. |
28 Февраля 2004 22:32 Раздел каталога :: Ссылка на задачу
|