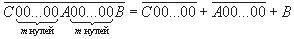358
476
всего разделов:
активных пользователей:
30 мартра 2005
Форумы снова функционируют.
21 декабря 2004
Видимо в связи с обнаруженными дырами в phpBB, форум был взломан, а через него взломано и всё остальное содержимое ceemat.ru. Всё кроме форума восстановлено, ведется дискуссия по поводу его сохранения.
Приносим извинения за неудобства.
29 сентября 2004
Форум обновился до версии 2.0.10
15 мая 2004
Новый раздел: "Программирование"
16 апреля 2004 года
Задачи Ярославского турнира математических боев — 124 задачи с решениями.
29 марта 2004
Таллинская викторина: занимательные вопросы и задачи для увлеченных химией.
Вторая лига (8)
Докажите, что для любой натуральной степени двойки найдется натуральный палиндром, который на нее делится. (Палиндромы — это числа, не меняющееся при прочтении справа налево, например, 1, 717, 2002). |
Докажем утверждение методом математической индукции. Любое четное число, являющееся палиндромом, делится на 2. Пусть A — палиндром, кратный 2k, B = 2k+1, C — число 2k+1, записанное справа налево. Тогда можно подобрать такое число m, что палиндром
делится на 2k+1, так как является суммой чисел, кратных 2k+1 (при достаточно большом значении m). |
Автор: А. Шаповалов. |
28 Февраля 2004 22:18 Раздел каталога :: Ссылка на задачу
|