358
475
всего разделов:
активных пользователей:
30 мартра 2005
Форумы снова функционируют.
21 декабря 2004
Видимо в связи с обнаруженными дырами в phpBB, форум был взломан, а через него взломано и всё остальное содержимое ceemat.ru. Всё кроме форума восстановлено, ведется дискуссия по поводу его сохранения.
Приносим извинения за неудобства.
29 сентября 2004
Форум обновился до версии 2.0.10
15 мая 2004
Новый раздел: "Программирование"
16 апреля 2004 года
Задачи Ярославского турнира математических боев — 124 задачи с решениями.
29 марта 2004
Таллинская викторина: занимательные вопросы и задачи для увлеченных химией.
Высшая лига и лига 9 классов (8)
Какое наибольшее число клеток шахматной доски можно отметить так, чтобы центры никаких четырех отмеченные клетки не были вершинами прямоугольника со сторонами, параллельными краям доски? |
Ответ: 24 клетки.
Рассмотрим произвольную вертикаль доски, пусть на ней отмечено k клеток, они образуют k × (k – 1) : 2 пар. Будем говорить, что пара отмеченных клеток покрывает пару горизонталей, на которых эти клетки находятся. Запрещенная четверка возникает, когда пара горизонталей будет покрыта дважды. Всего имеется 28 пар горизонталей. Если на вертикали отмечены 0, 1, 2, 3, 4, 5, 6, 7 или 8 клеток, то они покроют соответственно 0, 0, 1, 3, 6, 10, 15, 21 или 28 пар горизонталей. Разности во второй последовательности возрастают. Из этого следует, что если максимум отмеченных точек на вертикали не менее чем на два более минимума, то при перекидывании клетки с максимальной вертикали на минимальную вертикаль суммарное количество пар клеток уменьшится, по крайней мере, на 1. Таким образом, минимум пар при данном числе отмеченных клеток достигается, когда максимальное количество клеток на вертикали отличается от минимального количества не более чем на 1. Допустим, что отмечено не менее 25 клеток. Оставим только 25 отмеченных клеток. Случай 1. Пусть есть вертикаль, где отмечено не более двух клеток. Вычеркнем ее и повернем доску на прямой угол. Тогда у нас имеется 7 горизонталей, то есть 21 пара горизонталей. С другой стороны, распределение 23 клеток дадут 7 вертикалей с тремя клетками и 1 вертикаль с 2 клетками, то есть 7 × 3 + 1 = 22 отмеченные пары. По принципу Дирихле найдется дважды покрытая пара. Случай 2. Пусть в каждой вертикали отмечено не менее трех клеток. Тогда есть 7 вертикалей с тремя клетками (“троек”) и одна вертикаль с четырьмя отмеченными клетками (“четверка”). Всего покрываются 7 × 3 + 6 = 27 пар горизонталей (противоречия пока нет, так как всего имеется 28 пар горизонталей). Покажем, что некоторые пары обязаны остаться непокрытыми. Каждая горизонталь входит в 7 пар, то есть в нечетное число. Если на ней отмеченная клетка на пересечении с “тройкой”, то покрываются две пары. Значит, если горизонталь не имеет отмеченной клетки в пересечении с “четверкой”, то остается как минимум одна непокрытая пара с участием этой горизонтали. “Четверка” не имеет отмеченных клеток в пересечении с четырьмя горизонталями, то есть найдутся две непокрытые пары горизонталей. Значит, покрыто максимум 26 пар из 28 возможных пар. По принципу Дирихле найдется дважды покрытая пара. |
Автор: А. Шаповалов. |
25 Февраля 2004 22:52 Раздел каталога :: Ссылка на задачу
|
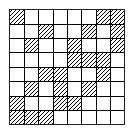 На рисунке показано, как можно отметить 24 клетки. Покажем, что более 24 клеток отметить нельзя.
На рисунке показано, как можно отметить 24 клетки. Покажем, что более 24 клеток отметить нельзя.