358
476
всего разделов:
активных пользователей:
30 мартра 2005
Форумы снова функционируют.
21 декабря 2004
Видимо в связи с обнаруженными дырами в phpBB, форум был взломан, а через него взломано и всё остальное содержимое ceemat.ru. Всё кроме форума восстановлено, ведется дискуссия по поводу его сохранения.
Приносим извинения за неудобства.
29 сентября 2004
Форум обновился до версии 2.0.10
15 мая 2004
Новый раздел: "Программирование"
16 апреля 2004 года
Задачи Ярославского турнира математических боев — 124 задачи с решениями.
29 марта 2004
Таллинская викторина: занимательные вопросы и задачи для увлеченных химией.
Первая лига (10)
| Страницы: « 1 2 | |
6. | Можно ли раскрасить натуральный ряд в 4 цвета так, чтобы для любого натурального n числа n, 2n, 3n и 4n были окрашены в разные цвета? |
17 Февраля 2004 17:59 | |
7. | Даны 6 точек в пространстве, никакие 4 из которые не лежат на одной плоскости. Докажите, что их можно разбить на две тройки так, что контуры двух треугольников с вершинами в точках каждой из троек будут зацеплены. |
17 Февраля 2004 17:44 | |
8. | Дан остроугольный треугольник ABC и точка M внутри него.
Длины сторон треугольника равняются a, b и c.
|
17 Февраля 2004 17:45 | |
9. | В каждой клетке таблицы n × n записано по -1, кроме того, фиксированы натуральные числа k и l, меньшие n. Разрешается одновременно поменять знаки у всех чисел, образующих прямоугольник k × l. Докажите, что сделать все числа равными +1 возможно только тогда, когда число n делится как на k, так и на l. |
17 Февраля 2004 17:46 | |
10. | Во вписанном четырехугольнике ABCD точка K — середина стороны AD, а ÐABK = ÐDCK. Докажите, что AB = CD. |
17 Февраля 2004 18:00 | |
| Страницы: « 1 2 | |
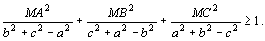 .
.