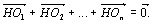358
476
всего разделов:
активных пользователей:
30 мартра 2005
Форумы снова функционируют.
21 декабря 2004
Видимо в связи с обнаруженными дырами в phpBB, форум был взломан, а через него взломано и всё остальное содержимое ceemat.ru. Всё кроме форума восстановлено, ведется дискуссия по поводу его сохранения.
Приносим извинения за неудобства.
29 сентября 2004
Форум обновился до версии 2.0.10
15 мая 2004
Новый раздел: "Программирование"
16 апреля 2004 года
Задачи Ярославского турнира математических боев — 124 задачи с решениями.
29 марта 2004
Таллинская викторина: занимательные вопросы и задачи для увлеченных химией.
Высшая лига (10)
| Страницы: « 1 2 | |
6. | Дан правильный многоугольник A1A2…An и точка O.
Точки O1, O2, …, On — образы точки O
при симметрии относительно прямых (A1A2), (A2A3), …, (AnA1),
точка H — центр многоугольника.
|
16 Февраля 2004 21:54 | |
7. | У прямоугольного параллелепипеда 1 × 1 × b окрасили одну грань 1 × b и положили его на плоскость этой гранью вниз. Может ли он после 1999 перекатываний оказаться на том же месте, но окрашенной гранью вверх? |
16 Февраля 2004 21:55 | |
8. | Не более 10% жителей некоторой страны — враги народа. Известно, что у каждого гражданина этой страны менее 500 знакомых. На день рождения президента каждый гражданин страны сделал ему подарок: написал в ДГБ письмо с разоблачением одного из знакомых ему врагов народа. При этом известно, что честные граждане разоблачали только истинных врагов, а враги могли как разоблачить других врагов, так и оклеветать честных граждан. Докажите, что на основании полученных данных ДГБ может посадить некоторое количество граждан так, чтобы больше половины посаженных была врагами народа. |
16 Февраля 2004 21:56 | |
9. | Все натуральные числа раскрашены в розовый и голубой цвета так, что чисел каждого цвета бесконечно много. Докажите, что существует число, являющееся и суммой двух розовых, и суммой двух голубых. |
16 Февраля 2004 22:12 | |
10. | На клетчатом поле n × n (n > 3) двое по очереди делают ходы. Первый игрок за один ход выставляет не более трех фишек (каждая — черная или белая по желанию игрока) на любые свободные поля. Второй игрок за один ход может переставить одну из стоящих на поле фишек на любое свободное поле. Если в какой-то момент образовались три (или более) фишки одного цвета, идущие подряд (по вертикали, горизонтали или диагонали), они снимаются с доски. Первый выигрывает, если все поля доски оказались заняты. Второй выигрывает, если какая-то позиция повторилась. Кто выиграет при правильной игре? |
16 Февраля 2004 21:56 | |
| Страницы: « 1 2 | |