358
476
всего разделов:
активных пользователей:
30 мартра 2005
Форумы снова функционируют.
21 декабря 2004
Видимо в связи с обнаруженными дырами в phpBB, форум был взломан, а через него взломано и всё остальное содержимое ceemat.ru. Всё кроме форума восстановлено, ведется дискуссия по поводу его сохранения.
Приносим извинения за неудобства.
29 сентября 2004
Форум обновился до версии 2.0.10
15 мая 2004
Новый раздел: "Программирование"
16 апреля 2004 года
Задачи Ярославского турнира математических боев — 124 задачи с решениями.
29 марта 2004
Таллинская викторина: занимательные вопросы и задачи для увлеченных химией.
Исходные задачи (15)
| Страницы: 1 | |
1. | В седьмом часу вечера Петя взглянул на часы: минутная стрелка была ровно на три минутных деления впереди часовой стрелки. Какое время показывали часы? |
17 Февраля 2004 20:13 | |
2. | Найдите хотя бы одно решение уравнения
в натуральных числах. |
17 Февраля 2004 20:13 | |
3. | Последовательность чисел задана следующим образом: a1 = 19, a2 = 99,
Найдите a1999. |
17 Февраля 2004 20:14 | |
4. | Какое наименьшее число авиалиний понадобится для того, чтобы из любого города из 1999 данных можно было добраться в любой другой, сделав не более двух пересадок? |
17 Февраля 2004 20:14 | |
5. | В результате измерения четырех сторон и одной из диагоналей некоторого
четырехугольника получились числа 1; 2; 2,8; 5; 7,5.
|
17 Февраля 2004 20:14 | |
6. | При стрельбе по мишени Миша несколько раз попал в десятку, столько же раз
выбил по 8 очков и несколько раз попал в пятерку. Всего он набрал 99 очков.
|
17 Февраля 2004 20:15 | |
7. | Вычислите:
|
17 Февраля 2004 20:18 | |
8. | Девяносто девять прямых разбивают плоскость на n частей.
|
17 Февраля 2004 20:19 | |
9. | Какое наибольшее количество чисел можно выбрать из набора 1, 2, …, 1999, чтобы сумма двух любых выбранных делилась на 36? |
17 Февраля 2004 20:19 | |
10. | В озере плавает яблоко: 2/3 его под водой и 1/3 над водой. К нему подплывает рыбка и подлетает птичка, которые одновременно начинают его есть, причем птичка ест вдвое быстрее, чем рыбка. Какую часть яблока съест птичка? |
17 Февраля 2004 20:21 | |
11. |
|
17 Февраля 2004 20:22 | |
12. | Не меняя порядка цифр, расставьте между цифрами числа 524127 знаки арифметических действий и скобки так, чтобы в итоге получилось 100. |
17 Февраля 2004 20:24 | |
13. | Сколько существует пар (a, b) натуральных чисел меньших 1999, таких, что a2 + b2 делится на 49? |
17 Февраля 2004 20:24 | |
14. | Найдите все натуральные числа, на которые можно сократить дробь
|
17 Февраля 2004 20:25 | |
15. | Сколько существует натуральных чисел, не больших 1999, которые не делятся ни на 5, ни на 7? |
17 Февраля 2004 20:26 | |
| Страницы: 1 | |
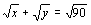
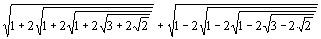
 Три окружности проходят через одну точку. Найдите сумму криволинейных углов
А, В, С в заштрихованной части большей окружности
Три окружности проходят через одну точку. Найдите сумму криволинейных углов
А, В, С в заштрихованной части большей окружности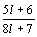 при различных целых значениях l.
при различных целых значениях l.