358
475
всего разделов:
активных пользователей:
30 мартра 2005
Форумы снова функционируют.
21 декабря 2004
Видимо в связи с обнаруженными дырами в phpBB, форум был взломан, а через него взломано и всё остальное содержимое ceemat.ru. Всё кроме форума восстановлено, ведется дискуссия по поводу его сохранения.
Приносим извинения за неудобства.
29 сентября 2004
Форум обновился до версии 2.0.10
15 мая 2004
Новый раздел: "Программирование"
16 апреля 2004 года
Задачи Ярославского турнира математических боев — 124 задачи с решениями.
29 марта 2004
Таллинская викторина: занимательные вопросы и задачи для увлеченных химией.
Осень 2000 года (25)
|
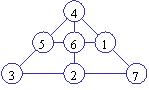
Вот одна из возможны расстановок:
Ответ пункта (б): сумма принимает единственное значение 12. Сумма всех чисел от 1 до 7 рана 28. Если в верхний кружок ставить одно из этих чисел, то сумма оставшихся шести чисел должна делиться на 2 (так как они располагаются на двух горизонтальных прямых) и на три (так как они расположены на трех вертикальных прямых). В таком случае в верхний кружочек можно поставить только число 4 (в этом не трудно убедиться, перебрав числа от 1 до 7). Тогда сумма чисел, расположенных на одной прямой равна (28 – 4) : 2 = 12 и других значений сумма принимать не может. Ответ пункта (в): 12 способов. Количество способов не зависит от числа, стоящего в верхнем кружочке, так как в нем может стоять только одно число 4. Остальные шесть чисел разбиваются на три пары с одинаковой суммой 8 (1 + 7, 2 + 6, 3 + 4). Так как число 8 можно представить в виде суммы двух чисел от 1 до 7 только этими тремя способами, то количество способов расставить числа в кружочки зависит от количества перестановок этих пар. Эти пары можно менять местами 6 способами (если одна пара стоит на первом месте, то две другие можно поставить на оставшиеся места двумя способами, а так как пар всего три, то способов — 6). Поменяем местами верхний и нижний ряд чисел и получим еще 6 перестановок пар. Таким образом, всего способов 12. |
5 Февраля 2004 22:37 Раздел каталога :: Ссылка на задачу
|
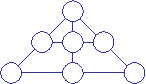 В кружочки расставляют числа
1, 2, 3, 4, 5, 6, 7 так, чтобы суммы чисел, стоящих на одной прямой, были равны
(в каждой сумме по три числа).
В кружочки расставляют числа
1, 2, 3, 4, 5, 6, 7 так, чтобы суммы чисел, стоящих на одной прямой, были равны
(в каждой сумме по три числа).