Осень 2000 года (25)

Решение. Разрезая квадрат на две или три части, какие–то две соседние вершины квадрата будут принадлежать одному меньшему квадрату, но тогда этот меньший квадрат совпадает с исходным квадратом. Поэтому на два и три квадрата разрезать нельзя.

Докажем, что квадрат нельзя разрезать на 5 квадратов. Так как две соседние вершины квадрата не могут принадлежать меньшему квадрату, то к каждой вершине исходного квадрата примыкает маленький квадрат, а пятый квадрат либо примыкает к одной из сторон квадрата, либо находится где-то в центре.

Если этот квадрат примыкает к одной из сторон исходного квадрата, то к этой стороне примыкает три квадрата. Рассмотрим противоположную сторону, к которой примыкает два квадрата.

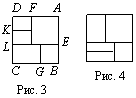
Если эти два квадрата равны между собой, то и их стороны равны: AF = AE = BE = BG = a (рис. 2). Так как ABCD — квадрат, то CG = a и DF = a. К стороне CD примыкают квадраты. Следовательно, CL = a и DK = a. Но тогда KL = 0, что невозможно.

Если же квадраты, примыкающие к стороне AB не равны, то остальные три квадрата располагаются как на рисунках 3 и 4. Рассмотрим рисунок 3.

Пусть AE = AF = a, BG = BE = b. Тогда сторона квадрата ABCD равна a + b. Получаем, что DF = DK = b, CG = CL = a и KL = 0, что невозможно. Случай на рисунке 4 рассматривается аналогично.

Если пятый квадрат находится где-то в центре, то остальные квадраты располагаются как на рисунке 5. Пусть BL = a, LC = b и сторона квадрата ABCD = a + b. Тогда KB = a, AK = b, AN> = b, ND = a, DM = a, MC = b. Сторону пятого квадрата можно вычислить как MD – AK = a – b или LC – ND = b – a. Получаем, что a – b = b – a, то есть a = b и тогда сторона пятого квадрата равна нулю, что невозможно.

Таким образом, квадрат нельзя разрезать на пять квадратов.