358
476
всего разделов:
активных пользователей:
30 мартра 2005
Форумы снова функционируют.
21 декабря 2004
Видимо в связи с обнаруженными дырами в phpBB, форум был взломан, а через него взломано и всё остальное содержимое ceemat.ru. Всё кроме форума восстановлено, ведется дискуссия по поводу его сохранения.
Приносим извинения за неудобства.
29 сентября 2004
Форум обновился до версии 2.0.10
15 мая 2004
Новый раздел: "Программирование"
16 апреля 2004 года
Задачи Ярославского турнира математических боев — 124 задачи с решениями.
29 марта 2004
Таллинская викторина: занимательные вопросы и задачи для увлеченных химией.
Весна 2000 года (25)
Как в вершинах куба расставить натуральные числа так, чтобы в каждой паре чисел, связанных ребром, одно из них делилось на другое, а во всех других парах такого не было? |
Пусть нам удалось расставить числа. На каждом ребре поставим стрелку к делителю. Если в какую-то вершину A входит стрелка (из вершины B) и выходит стрелка (в вершину C), то число в вершине B будет делится на число в вершине C, что противоречит условию (так как вершины B и C не будут соседними). Значит, из любой вершины из либо все стрелки выходят, либо входят в нее. Такая расстановка стрелок единственная (рисунок 13).
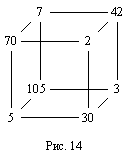
Исходя из этого, расстановку чисел можно получить так: в вершины, в которые стрелки входят, поместить различные простые числа, а в каждую из остальных — произведение чисел в соседних по ребру вершинах. Пример расстановки показан на рисунке 14.
|
3 Февраля 2004 21:04 Раздел каталога :: Ссылка на задачу
|