358
476
всего разделов:
активных пользователей:
30 мартра 2005
Форумы снова функционируют.
21 декабря 2004
Видимо в связи с обнаруженными дырами в phpBB, форум был взломан, а через него взломано и всё остальное содержимое ceemat.ru. Всё кроме форума восстановлено, ведется дискуссия по поводу его сохранения.
Приносим извинения за неудобства.
29 сентября 2004
Форум обновился до версии 2.0.10
15 мая 2004
Новый раздел: "Программирование"
16 апреля 2004 года
Задачи Ярославского турнира математических боев — 124 задачи с решениями.
29 марта 2004
Таллинская викторина: занимательные вопросы и задачи для увлеченных химией.
M781 - M800 (20)
M793*
Из вершины P тетраэдра PАВС проводятся три отрезка PA', PB', PC', перпендикулярные граням PВС, PСА, PАВ и равные по длине площадям этих граней соответственно (направления отрезков выбираются так, что точки A' и А, B' и B, C' и С лежат по разные стороны плоскостей соответствующих граней PВС, PСА, PАВ (показано на рисунке). Докажите, что а) повторив это же построение для тетраэдра (и его вершины P), мы получим тетраэдр, гомотетичный исходному тетраэдру PАВС с коэффициентом 3V/4, где V равно объему тетраэдра PАВС; б) вектор в) Из точки O, взятой внутри тетраэдра АВСD, опускаются перпендикуляры на плоскости его граней. На этих перпендикулярах от точки O откладываются отрезки, равные по длине площадям соответствующих граней, и концы этих отрезков принимаются за вершины нового тетраэдра А'В'С'D'. (Разумеется, с точностью до параллельного переноса, этот тетраэдр не зависит от выбора точки O.) Докажите, что, повторив это построение для тетраэдра А'В'С'D', мы получим тетраэдр, гомотетичный исходному с коэффициентом 3V, где V — объем исходного тетраэдра АВСD. (Если 3V = 1, то последний тетраэдр получается из исходного параллельным переносом.) |
27 Января 2004 22:24 Раздел каталога :: Ссылка на задачу
|
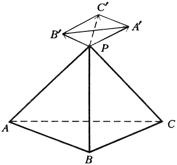
 перпендикулярен плоскости АВС.
перпендикулярен плоскости АВС.