358
476
всего разделов:
активных пользователей:
30 мартра 2005
Форумы снова функционируют.
21 декабря 2004
Видимо в связи с обнаруженными дырами в phpBB, форум был взломан, а через него взломано и всё остальное содержимое ceemat.ru. Всё кроме форума восстановлено, ведется дискуссия по поводу его сохранения.
Приносим извинения за неудобства.
29 сентября 2004
Форум обновился до версии 2.0.10
15 мая 2004
Новый раздел: "Программирование"
16 апреля 2004 года
Задачи Ярославского турнира математических боев — 124 задачи с решениями.
29 марта 2004
Таллинская викторина: занимательные вопросы и задачи для увлеченных химией.
M781 - M800 (20)
M790 а) Про числовую функцию f известно, что если
Пусть про отображение F плоскости в себя известно, что любые две точки X, Y,
находящиеся на расстоянии 1, оно переводит в две точки
Тогда для любых двух точек X, Y плоскости
б) ρ(F(X),F(Y)) £ ρ(X, Y) + 1; в)* ρ(X, Y) = г)* ρ(F(X),F(Y)) £ ρ(X, Y);; д)* ρ(F(X),F(Y)) ³ ρ(X, Y);. (Вы можете, конечно, предложить и другой план доказательства теоремы.) |
27 Января 2004 21:44 Раздел каталога :: Ссылка на задачу
|
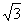 ;
Þ
ρ(F(X),F(Y)) =
;
Þ
ρ(F(X),F(Y)) =