358
476
всего разделов:
активных пользователей:
30 мартра 2005
Форумы снова функционируют.
21 декабря 2004
Видимо в связи с обнаруженными дырами в phpBB, форум был взломан, а через него взломано и всё остальное содержимое ceemat.ru. Всё кроме форума восстановлено, ведется дискуссия по поводу его сохранения.
Приносим извинения за неудобства.
29 сентября 2004
Форум обновился до версии 2.0.10
15 мая 2004
Новый раздел: "Программирование"
16 апреля 2004 года
Задачи Ярославского турнира математических боев — 124 задачи с решениями.
29 марта 2004
Таллинская викторина: занимательные вопросы и задачи для увлеченных химией.
М741 - М760 (20)
| Страницы: 1 | |
1. | M741 а) Найдите хотя бы одно натуральное число, которое делится на 30 и имеет ровно 30 различных делителей (включая 1 и само число). б) Укажите все такие числа. |
18 Января 2004 21:07 | |
2. | M742 На а) окружности, б) сфере радиусом 1 расположены n точек. Докажите, что сумма квадратов попарных расстояний между ними не больше n2. |
18 Января 2004 21:08 | |
3. | M743 В стране N городов. а) Между любыми двумя городами имеется прямое сообщение самолетом или пароходом. Докажите, что, пользуясь лишь каким-то одним видом транспорта, из любого города можно попасть в любой другой (возможно, с пересадками). б) Между любыми двумя городами имеется прямое сообщение самолетом, поездом или пароходом. Докажите, что можно выбрать не менее N/2 городов и один из трех видов транспорта так, что, пользуясь им одним, из любого выбранного города можно попасть в любой другой выбранный город. в) Приведите пример, доказывающий, что в утверждении б) заменить число N/2 большим, вообще говоря, нельзя. |
18 Января 2004 21:10 | |
4. | M744* В треугольник АВС вписан подобный ему треугольник А1В1С1 (вершины А1, В1, С1 углов, равных по величине ÐА, ÐB, ÐC, лежат соответственно на отрезках ВС, СА и АВ). Пусть А0, В0, С0 — точки пересечения прямых BВ1 и CС1, АA1 и CС1, BB1 и AA1. Докажите, что шесть окружностей, описанных около треугольников АВС0, ВСA0, АСB0, А1В1С0, А1В1С0, А1В1С0, пересекаются в одной точке. |
18 Января 2004 21:11 | |
5. | M745* а) Задана последовательность чисел (dn) таких, что ½dn½£1 (n = 1, 2, ...). Докажите, что можно выбрать последовательность (sn) из чисел +1 и -1 так, что для всех n выполняется неравенство ½d1s1 + d2s2 +...+ dnsn½£1. б) Задана последовательность троек чисел (an, bn, cn) таких, что ½an½£1, ½bn½£1, ½cn½£1, и an + bn + cn = 0 (n = 1, 2, ...). По ней строится новая последовательность троек (xn, yn, zn), в которой xn = yn = zn = 0 , а каждая тройка (xn, yn, zn) при n³1 получается из предыдущей (xn-1, yn-1, zn-1) путем прибавления к xn-1 одного из чисел по нашему выбору, к yn-1 – другого, к zn-1 - третьего. Можем ли мы всегда добиться того, что все числа xn, yn, zn будут по абсолютной величине не больше 1 или хотя бы ограничены некоторой константой? в) Выясните аналогичные вопросы для последовательностей четверок чисел. |
18 Января 2004 21:12 | |
6. | M746
а) полученный девятиугольник имел наибольшую площадь? б)* в нем помещалась окружность наибольшего возможного радиуса (показано на рисунке)? |
18 Января 2004 21:14 | |
7. | M747 а) Сумма n чисел равна 0, сумма их модулей равна a. Докажите, что разность между наибольшим и наименьшим из них не меньше 2a/n. б)* Внутри выпуклого n-угольника
А1A2A3...An
выбрана точка O так, что сумма векторов
в)* Можно ли улучшить эту оценку (при некоторых n)? |
18 Января 2004 21:15 | |
8. | M748
б)* В пространстве расположено несколько непересекающихся конусов. Докажите, что их нельзя переместить так, чтобы они покрыли все пространство. (Конусом мы называем здесь неограниченную выпуклую фигуру, полученную в результате вращения некоторого угла вокруг его биссектрисы.) |
18 Января 2004 21:16 | |
9. | M749* а) Докажите, что если x1, x2, x3 —
положительные числа, то б) Докажите, что если x1, x2, ..., xn —
положительные числа, то
в) Докажите, что при n > 4 неравенство пункта б) является точным в том смысле, что ни при каком n число 2 в правой части нельзя заменить на большее. |
18 Января 2004 21:17 | |
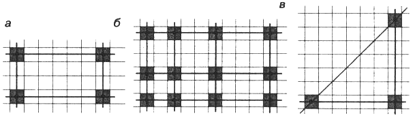
10. | M750 Докажите, что как бы ни раскрасить клетки бесконечного листа клетчатой бумаги в N цветов, найдутся а) прямоугольник, вершины которого лежат в центрах клеток одного цвета (а стороны идут параллельно линиям сетки — по горизонтальным и вертикальным прямым — см. рисунок а); б) l горизонтальных и m вертикальных прямых, которые пересекаются в центрах lm клеток одного цвета (l и m — любые натуральные числа — см. рисунок б);
в) равнобедренный прямоугольный треугольник, вершины которого — центры клеток одного цвета, при N = 2 (показано на рисунке в); г)* то же для N = 3. |
18 Января 2004 21:18 | |
11. | M751* На окружности намечены 3k точек, разделяющих ее на 3k дуг, из которых k дуг имеют длину 1, еще k дуг — длину 2, и остальные k дуг — длину 3. Докажите, что среди отмеченных точек найдутся две диаметрально противоположные. |
18 Января 2004 21:19 | |
12. | M752 Квадратная таблица n×n клеток заполнена целыми числами. При этом в клетках, имеющих общую сторону, записаны числа, отличающиеся друг от друга не больше, чем на 1. Докажите, что хотя бы одно число встречается в таблице: а) не менее чем [n/2] раз ([a] — целая часть a); б) не менее чем n раз. |
18 Января 2004 21:20 | |
13. | M753 Числа a, b, c лежат на интервале (0, p/2) и удовлетворяют равенствам: cos a = a, sin cos b = b, cos sin c = c. Расположите числа в порядке возрастания. |
18 Января 2004 21:21 | |
14. | M754* а) Существуют ли многочлены P = P(x, y, z),
Q = Q(x, y, z), R = R(x, y, z)
от переменных x, y, z такие, что выполнено тождество б) тот же вопрос для тождества |
18 Января 2004 21:23 | |
15. | M755 Внутри тетраэдра выбрана точка M. Докажите, что хотя бы одно ребро тетраэдра видно из точки M под углом, косинус которого не больше чем –1/3. |
18 Января 2004 21:24 | |
16. | M756* В стране, кроме столицы, больше 100 городов. Столица страны соединена авиалиниями со 100 городами; каждый из остальных городов соединен авиалиниями ровно с 10 городами. Известно, что из любого города можно (быть может, с пересадками) перелететь в любой другой. Докажите, что можно закрыть половину авиалиний, идущих из столицы, так, что возможность попасть из любого города в любой сохранится. |
18 Января 2004 21:25 | |
17. | M757 Из последовательности 1, 1/2, 1/3, 1/4,... нетрудно выделить арифметическую прогрессию длиной 3: 1/2, 1/3, 1/6. Можно ли из этой последовательности выбрать арифметическую прогрессию а) длиной 4? б) длиной 5? в) длиной k, где k — любое натуральное число? |
18 Января 2004 21:25 | |
18. | M758* Какое наименьшее количество чисел можно вычеркнуть из последовательности 1, 2, 3,... 1982, чтобы ни одно из оставшихся чисел не равнялось произведению двух других оставшихся чисел? |
18 Января 2004 21:26 | |
19. | M759 Внутри выпуклого четырехугольника, у которого сумма шести попарных расстояний между вершинами (т.е. сумма длин всех сторон и диагоналей) равна S1, расположен другой, для которого эта сумма равна S2. a) Может ли величина S2 быть больше S1? б) Докажите, что S2 < 4S1/3. в) Докажите, что если внутри правильного тетраэдра с суммой длин ребер S1 расположен другой, для которого эта сумма равна S2, то S2 < 4S1/3. |
18 Января 2004 21:27 | |
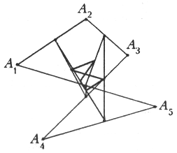
20. | M760
a) при m = 5 — через 2 шага (показано на рисунке), б) при m = 7 — через 3 шага, в) при любом нечетном m — через некоторое (зависящее от m) число шагов получится ломаная, подобная (даже гомотетичная) первоначальной. |
18 Января 2004 21:28 | |
| Страницы: 1 | |
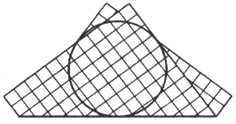 Бумажный квадрат складывается пополам по некоторой прямой l,
проходящей через его центр, в (невыпуклый) девятиугольник. Как нужно
провести прямую l, чтобы:
Бумажный квадрат складывается пополам по некоторой прямой l,
проходящей через его центр, в (невыпуклый) девятиугольник. Как нужно
провести прямую l, чтобы:
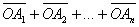 равна нулевому вектору, а сумма их длин равна d. Докажите, что периметр
этого n-угольника не меньше 4d/n.
равна нулевому вектору, а сумма их длин равна d. Докажите, что периметр
этого n-угольника не меньше 4d/n.
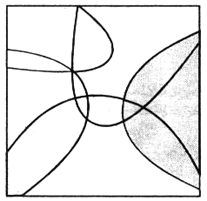 а) Можно ли разместить на плоскости конечное число парабол так, чтобы их
внутренние области покрыли всю плоскость? (Внутренней областью параболы
мы называем выпуклую фигуру, границей которой служит эта парабола — см. рисунок)
а) Можно ли разместить на плоскости конечное число парабол так, чтобы их
внутренние области покрыли всю плоскость? (Внутренней областью параболы
мы называем выпуклую фигуру, границей которой служит эта парабола — см. рисунок)
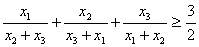 ;
;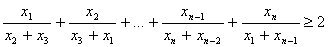 ;
;
 С замкнутой ломаной
A1A2...Am,
где m нечетно, проделывается такая операция: середины ее звеньев соединяются
m отрезками через одну
(середина A1A2 — с серединой A3A4,
A2A3 — с A4A5, ...,
Am-1Am — с A1A2,
AmA1 — с A2A3).
С полученной ломаной вновь проделывается эта же операция и т.д. Докажите, что из любой m-звенной ломаной
С замкнутой ломаной
A1A2...Am,
где m нечетно, проделывается такая операция: середины ее звеньев соединяются
m отрезками через одну
(середина A1A2 — с серединой A3A4,
A2A3 — с A4A5, ...,
Am-1Am — с A1A2,
AmA1 — с A2A3).
С полученной ломаной вновь проделывается эта же операция и т.д. Докажите, что из любой m-звенной ломаной