M681 - M700 (20)

11.

M691

Будем говорить, что число обладает свойством (К) , если оно разлагается в произведение К последовательных натуральных чисел, больших 1.

а) Найдите К такое, для которого некоторое число N обладает одновременно свойствами (К) и (К + 2).

б) Докажите, что чисел, обладающих одновременно свойствами (2) и (4), не существует.

12.

M692

Точки C₁, A₁, B₁ взяты на сторонах, соответственно, АВ, ВС, СА треугольника ABC так, что АС₁ : С₁В = ВA₁ : A₁С = CB₁ : BA₁ = 1 : 3. Докажите, что периметр Р треугольника AВС и периметр Р₁ треугольника А₁В₁С₁ связаны неравенствами

а) Р₁<3/4P;

б) Р₁>1/2P.

13.

M693

В некотором поселке 1000 жителей. Ежедневно каждый из них делится узнанными накануне новостями со всеми своими знакомыми. Известно, что любая новость становится известной всем жителям поселка. Докажите, что можно выбрать 90 жите лей так, что если одновременно всем им сообщить какую-то новость, то через 10 дней она станет известной всем жителям поселка.

14.

M694

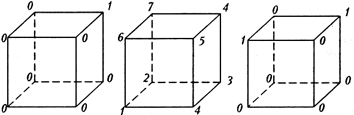
В каждой вершине куба записано число. За один шаг к двум числам, размещенным на одном (любом) ребре, прибавляется по единице. Можно ли за несколько таких шагов сделать все восемь чисел равными между собой, если вначале были поставлены числа, как на рисунке слева? как на среднем рисунке? как на рисунке справа?

15.

M695*

Можно ли все клетки какой-нибудь прямоугольной таблицы окрасить в белый и черный цвета так, чтобы черных и белых клеток было поровну, а в каждой строке и в каждом столбце было более 3/4 клеток одного цвета?

16.

M696

Mожно ли таблицу 10 × 10 клеток заполнить 100 различными натуральными числами так, чтобы для любого квадрата k × k клеток (2£ k£ 10)

а) суммы,

б) произведения k чисел на его диагоналях были одинаковы?

17.

M697

Назовем пузатостью прямоугольника отношение его меньшей стороны к большей (пузатость квадрата равна 1). Докажите, что, как бы ни разрезать квадрат на прямоугольники, сумма их пузатостей будет не меньше 1.

18.

M698

На сторонах a, b, c, d вписанного в окружность четырехугольника «наружу» построены прямоугольники размерами a×c, b×d, c×a, d×b. Докажите, что центры этих прямоугольников являются вершинами

а) параллелограмма,

б) прямоугольника.

19.

M699

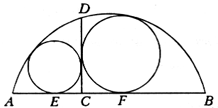
Полукруг с диаметром АВ разрезан отрезком СО, перпендикулярным АВ, на два криволинейных треугольника ACD и BCD, в которые вписаны окружности, касающиеся АВ в точках Е и F (показано на рисунке). Докажите, что

а) AD = AF;

б) DF — биссектриса угла BDC;

в) величина угла EDF не зависит от выбора точки С на АВ.

20.

M700

Можно ли множество всех конечных десятичных дробей разбить на а) два, 6) три класса так, чтобы в один класс не попали два числа с разностью 10^m (ни при каком целом m = 0, ±1, ±2, ...)?