358
476
всего разделов:
активных пользователей:
30 мартра 2005
Форумы снова функционируют.
21 декабря 2004
Видимо в связи с обнаруженными дырами в phpBB, форум был взломан, а через него взломано и всё остальное содержимое ceemat.ru. Всё кроме форума восстановлено, ведется дискуссия по поводу его сохранения.
Приносим извинения за неудобства.
29 сентября 2004
Форум обновился до версии 2.0.10
15 мая 2004
Новый раздел: "Программирование"
16 апреля 2004 года
Задачи Ярославского турнира математических боев — 124 задачи с решениями.
29 марта 2004
Таллинская викторина: занимательные вопросы и задачи для увлеченных химией.
M661 - M680 (20)
| Страницы: « 1 2 | |
11. | M671 Во вписанном четырехугольнике одна диагональ делит вторую пополам. Докажите, что квадрат длины первой диагонали равен половине суммы квадратов длин всех сторон четырехугольника. |
15 Января 2004 21:52 | |
12. | M672 Пусть a — натуральное число такое, что 2a - 2 делится на a (например, a = 3). Определим последовательность (xn) условиями |
15 Января 2004 21:52 | |
13. | M673 На плоскости в вершинах треугольника лежат три шайбы A, B и C. Хоккеист выбирает одну из них и бьет по ней так, что она проходит между двумя другими и останавливается в какой-то точке. а) Покажите, как после пяти ударов шайба C сможет вернуться на свое место, а шайбы A и B поменяться местами. б) Могут ли все три шайбы A, B и C вернуться на свои прежние места после 25 ударов? |
15 Января 2004 21:53 | |
14. | M674 На сторонах BC, AC и AB остроугольного треугольника ABC взяты точки A1, B1 и C1 соответственно. Известно, что центр описанной около треугольника ABC окружности совпадает с точкой пересечения высот треугольника A1B1C1. Докажите, что треугольники ABC и A1B1C1 подобны. |
15 Января 2004 21:53 | |
15. | M675* Системой разновесов называется совокупность натуральных чисел, из которой нельзя извлечь два различных набора с одинаковой суммой (например, числа 24, 23, 22, 20, 17, 11 образуют систему разновесов, а числа 1, 2, 3, 4, 5, 8 не образуют: 2 + 3 + 4 = 1 + 8). Докажите, что из чисел, меньших 1000, можно выделить систему разновесов из |
15 Января 2004 21:53 | |
16. | M676 Докажите, что для любого натурального n сумма цифр числа 1981m не меньше 19. |
15 Января 2004 21:53 | |
17. | M677 Внутри остроугольного треугольника АВС выбрана точка M, являющаяся Докажите, что если радиусы окружностей, вписанных в треугольники АМВ, МВС, АМС, равны, то треугольник АВС — правильный. |
15 Января 2004 21:54 | |
18. | M679
б) В пространстве расположены четыре шара так, что первый касается второго в точке A, второй — третьего в точке В, третий — четвертого в точке С. а четвертый — первого в точке D. Докажите, что четыре названные точки лежат в одной плоскости. в) Докажите, что в условиях предыдущей задачи эти четыре точки лежат на одной окружности или на одной прямой. |
15 Января 2004 21:54 | |
19. | M680* Два связиста играют в такую игру. Имеются n телефонных узлов, и связисты по очереди соединяют кабелем два из них по своему выбору. Выигрывает тот, после хода которого с любого узла можно будет дозвониться до любого другого (быть может, через несколько промежуточных; начало игры изображено на рисунке 3). а) Выясните, кто выигрывает при n = 4, 5, 6, 7, 8 — начинающий или его партнер? б) Каков ответ при произвольном n? в) Пусть игрок, связавший все узлы, проигрывает. Ответьте на вопросы пунктов а) и б) для этой новой игры. г) Пусть вначале все узлы попарно связаны кабелем, а связисты убирают по очереди по одному соединению. Игрок, нарушивший связь в схеме, проигрывает. Вопрос тот же: кто выигрывает при правильной стратегии для n = 4, 5, 6, 7, 8? А для произвольного n? Замечание. Можно было бы рассмотреть четвертый вариант: считать, что в пункте г) игрок, нарушивший связь, выигрывает. Полное исследование этого варианта игры неизвестно. |
15 Января 2004 21:55 | |
20. | M678 2m-значное число называется справедливым, если его четные разряды содержат столько же четных цифр, сколько и нечетные. Докажите, что в любом (2m + 1)-значном числе можно вычеркнуть одну из цифр так, чтобы полученное 2m-значное число было справедливым (показано на рисунке).
|
18 Января 2004 16:10 | |
| Страницы: « 1 2 | |
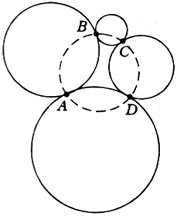 а) На плоскости расположены четыре круга так, что первый касается второго в точке A, второй — третьего в точке B, третий — четвертого в точке C, а четвертый — первого в точке D . (показано на рисунке). Докажите, что через четыре названные точки можно провести окружность или прямую.
а) На плоскости расположены четыре круга так, что первый касается второго в точке A, второй — третьего в точке B, третий — четвертого в точке C, а четвертый — первого в точке D . (показано на рисунке). Докажите, что через четыре названные точки можно провести окружность или прямую.