358
476
всего разделов:
активных пользователей:
30 мартра 2005
Форумы снова функционируют.
21 декабря 2004
Видимо в связи с обнаруженными дырами в phpBB, форум был взломан, а через него взломано и всё остальное содержимое ceemat.ru. Всё кроме форума восстановлено, ведется дискуссия по поводу его сохранения.
Приносим извинения за неудобства.
29 сентября 2004
Форум обновился до версии 2.0.10
15 мая 2004
Новый раздел: "Программирование"
16 апреля 2004 года
Задачи Ярославского турнира математических боев — 124 задачи с решениями.
29 марта 2004
Таллинская викторина: занимательные вопросы и задачи для увлеченных химией.
М1841 - М1860 (14)
| Страницы: 1 | |
1. | М1846 Докажите, что для любого натурального n и любого натурального k £ n выполняется неравенство
|
17 Января 2004 23:11 | |
2. | М1847 В 8 банках сидят 80 пауков. Разрешается выбрать любые две банки, суммарное число пауков в которых чётное, и пересадить часть пауков из одной банки в другую, чтобы их стало поровну. При любом ли начальном распределении пауков в банках с помощью нескольких таких операций можно добиться того, чтобы в каждой банке оказалось одинаковое число пауков? |
17 Января 2004 23:12 | |
3. | М1848 В треугольник АВС вписана окружность с центром О, которая касается сторон в точках А1, В1, С1. Отрезки АО, ВО, СО пересекают окружность в точках А2, В2, С2. Докажите, что площадь треугольника А2В2С2. равна половине площади шестиугольника В1А2С1В2А1С2. |
17 Января 2004 23:13 | |
4. | М1849 Простое число p удовлетворяет равенству
|
17 Января 2004 23:14 | |
5. | М1850 Числа натурального ряда от 1 до |
17 Января 2004 23:14 | |
6. | М1852 Дано натуральное число n. В интервале (n2; n2 + n) выбраны различные натуральные числа a и b. Докажите, что в этом интервале нет натуральных делителей числа |
29 Декабря 2003 19:26 | |
7. | М1853 С числом разрешается производить следующие операции: Можно ли с помощью таких операций из числа 81 получить число 82? |
29 Декабря 2003 19:23 | |
8. | М1854* Пусть |
29 Декабря 2003 19:23 | |
9. | М1855 Плоскости, параллельные граням прямоугольного параллелепипеда, разрезали его на меньшие параллелепипеды, которые окрасили в чёрный и белый цвета в шахматном порядке. Известно, что суммарный объём чёрных равен суммарному объёму белых параллелепипедов. Докажите, что из чёрных параллелепипедов можно составить параллелепипед P, а из белых можно составить параллелепипед Q так, что P и Q будут равны. |
29 Декабря 2003 19:24 | |
10. | M1856
|
29 Декабря 2003 19:24 | |
11. | M1857 На окружности находится множество К, состоящее из k точек, делящих окружность на k равных дуг. В К взяты два подмножества М и N, содержащие m и n точек соответственно. У подмножеств М и N ровно r общих точек. Более того, на какой бы угол, кратный 2π / k, мы ни повернули подмножество N, оно по прежнему будет иметь ровно r общих точек с подмножеством М. Докажите, что r=mn / k. |
17 Января 2004 23:05 | |
12. | М1858 Даны такие натуральные числа а и b, что 2а + 1 и 2b + 1 взаимно просты. Каким может быть наибольший общий делитель чисел |
29 Декабря 2003 19:25 | |
13. | М1859 Квадратный стол площади 2 можно в два слоя покрыть четырьмя квадратными салфетками, площадь каждой из которых равна 1. Более того, это можно сделать 100 различными способами. Найдите эти способы. (Салфетки можно перегибать, но нельзя разрывать). |
29 Декабря 2003 19:25 | |
14. | М1860
|
29 Декабря 2003 19:26 | |
| Страницы: 1 | |
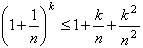
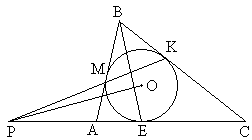 Окружность с центром О, вписанная в треугольник АВС, касается его основания АС в точке Е, а боковых сторон — в точках М и К (показано на рисунке). Прямая МК пересекает продолжение основания в точке Р. Докажите, что прямая РО перпендикулярна прямой ВЕ.
Окружность с центром О, вписанная в треугольник АВС, касается его основания АС в точке Е, а боковых сторон — в точках М и К (показано на рисунке). Прямая МК пересекает продолжение основания в точке Р. Докажите, что прямая РО перпендикулярна прямой ВЕ.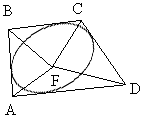 Точка F является одним из фокусов эллипса, вписанного в выпуклый четырёхугольник ABCD (показано на рисунке). Докажите, что сумма углов AFB и CFD равна 180
Точка F является одним из фокусов эллипса, вписанного в выпуклый четырёхугольник ABCD (показано на рисунке). Докажите, что сумма углов AFB и CFD равна 180