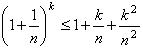358
476
всего разделов:
активных пользователей:
30 мартра 2005
Форумы снова функционируют.
21 декабря 2004
Видимо в связи с обнаруженными дырами в phpBB, форум был взломан, а через него взломано и всё остальное содержимое ceemat.ru. Всё кроме форума восстановлено, ведется дискуссия по поводу его сохранения.
Приносим извинения за неудобства.
29 сентября 2004
Форум обновился до версии 2.0.10
15 мая 2004
Новый раздел: "Программирование"
16 апреля 2004 года
Задачи Ярославского турнира математических боев — 124 задачи с решениями.
29 марта 2004
Таллинская викторина: занимательные вопросы и задачи для увлеченных химией.
М1841 - М1860 (14)
| Страницы: 1 2 3 » | |
1. | М1846 Докажите, что для любого натурального n и любого натурального k £ n выполняется неравенство
|
17 Января 2004 23:11 | |
2. | М1847 В 8 банках сидят 80 пауков. Разрешается выбрать любые две банки, суммарное число пауков в которых чётное, и пересадить часть пауков из одной банки в другую, чтобы их стало поровну. При любом ли начальном распределении пауков в банках с помощью нескольких таких операций можно добиться того, чтобы в каждой банке оказалось одинаковое число пауков? |
17 Января 2004 23:12 | |
3. | М1848 В треугольник АВС вписана окружность с центром О, которая касается сторон в точках А1, В1, С1. Отрезки АО, ВО, СО пересекают окружность в точках А2, В2, С2. Докажите, что площадь треугольника А2В2С2. равна половине площади шестиугольника В1А2С1В2А1С2. |
17 Января 2004 23:13 | |
4. | М1849 Простое число p удовлетворяет равенству
|
17 Января 2004 23:14 | |
5. | М1850 Числа натурального ряда от 1 до |
17 Января 2004 23:14 | |
| Страницы: 1 2 3 » | |