358
471
всего разделов:
активных пользователей:
30 мартра 2005
Форумы снова функционируют.
21 декабря 2004
Видимо в связи с обнаруженными дырами в phpBB, форум был взломан, а через него взломано и всё остальное содержимое ceemat.ru. Всё кроме форума восстановлено, ведется дискуссия по поводу его сохранения.
Приносим извинения за неудобства.
29 сентября 2004
Форум обновился до версии 2.0.10
15 мая 2004
Новый раздел: "Программирование"
16 апреля 2004 года
Задачи Ярославского турнира математических боев — 124 задачи с решениями.
29 марта 2004
Таллинская викторина: занимательные вопросы и задачи для увлеченных химией.
2. Отношение сторон подобных треугольников (17)
Задача 1.24 Пусть AC — большая из диагоналей параллелограмма ABCD. Из точки C на продолжения сторон AB и AD опущены перпендикуляры CE и CF соответственно. Докажите, что AB · AE + AD · AF = AC2. |
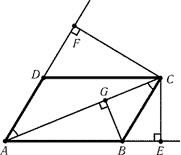 Опустим из вершины В перпендикуляр BG на AC. Из подобия треугольников ABG и ACE получаем AC · AG = AE · AB. Прямые AF и CB параллельны, поэтому углы GCB и CAF равны и прямоугольные треугольники CBG и ACF подобны. Из подобия этих треугольников получаем AC · CG = AF · BC. Складывая полученные равенства, находим AC · (AG + CG) = AE · AB + AF · BC. Так как AG + CG = AC, получаем требуемое равенство. |
17 Января 2004 14:55 Раздел каталога :: Ссылка на задачу
|