358
471
всего разделов:
активных пользователей:
30 мартра 2005
Форумы снова функционируют.
21 декабря 2004
Видимо в связи с обнаруженными дырами в phpBB, форум был взломан, а через него взломано и всё остальное содержимое ceemat.ru. Всё кроме форума восстановлено, ведется дискуссия по поводу его сохранения.
Приносим извинения за неудобства.
29 сентября 2004
Форум обновился до версии 2.0.10
15 мая 2004
Новый раздел: "Программирование"
16 апреля 2004 года
Задачи Ярославского турнира математических боев — 124 задачи с решениями.
29 марта 2004
Таллинская викторина: занимательные вопросы и задачи для увлеченных химией.
Осенний тур. Тренировочный вариант. 8-9 класс (5)
Итог подводился по трем задачам, по которым достигнуты наилучшие результаты, баллы за пункты одной задачи суммируются.
Стоимость задач
| Номер задачи | 1 | 2 | 3а | 3б | 3в | 4 | 5 |
| Баллы | 4 | 5 | 1 | 2 | 2 | 5 | 5 |
Дан некоторый угол и точка O внутри угла. Можно ли провести через точку O три прямые так, чтобы на каждой из сторон угла одна из точек пересечения этих прямых со стороной лежала посредине между двумя другими точками пересечения прямых с этой же стороной? |
Ответ: нельзя.
Значит, PQ / PO = YZ / OY = YX / OY = AP / PO, откуда, PQ = AP. Так как AB = BC, то прямые BP и CQ параллельны. Но они пересекаются в точке O. Противоречие. |
13 Декабря 2003 14:35 Раздел каталога :: Ссылка на задачу
|
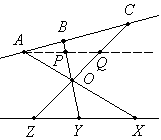Пусть AX, BY, CZ — данные прямые,
причем точки A, B, C лежат на одной стороне угла, а точки X, Y, Z —
на другой. Пусть AB = BC и ZY = YX. Проведем через точку A
прямую l, параллельную XZ. Пусть l пересекает прямые BY и CZ в точках
P и Q соответственно. Тогда треугольник APO подобен треугольнику XYO, а треугольник
PQO подобен треугольнику YZO.