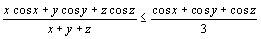358
476
всего разделов:
активных пользователей:
30 мартра 2005
Форумы снова функционируют.
21 декабря 2004
Видимо в связи с обнаруженными дырами в phpBB, форум был взломан, а через него взломано и всё остальное содержимое ceemat.ru. Всё кроме форума восстановлено, ведется дискуссия по поводу его сохранения.
Приносим извинения за неудобства.
29 сентября 2004
Форум обновился до версии 2.0.10
15 мая 2004
Новый раздел: "Программирование"
16 апреля 2004 года
Задачи Ярославского турнира математических боев — 124 задачи с решениями.
29 марта 2004
Таллинская викторина: занимательные вопросы и задачи для увлеченных химией.
Осенний тур. Тренировочный вариант. 10-11 класс (5)
Итог подводился по трем задачам, по которым достигнуты наилучшие результаты, баллы за пункты одной задачи суммируются.
Стоимость задач
| Номер задачи | 1 | 2а | 2б | 2в | 3 | 4 | 5 |
| Баллы | 2 | 1 | 1 | 2 | 5 | 5 | 5 |
Пусть x, y, z — любые числа из интервала (0; p/2).
|
Так как x + y + z > 0, то данное неравенство равносильно следующему: 3x × cos x + 3y × cos y + 3z × cos z £ (cos x + cos y + cos z) × (x + y + z). Раскрывая скобки и приводя подобные слагаемые, получим: 2x × cos x + 2y × cos y + 2z × cos z £
Неравенство (1) получается сложением неравенств (2), (3) и (4): x × cos x + y × cos y £ x × cos y + y × cos x, (2) x × cos x + z × cos z £ x × cos z + z × cos x, (3) y × cos y + z × cos z £ y × cos z + z × cos y. (4) Докажем неравенство (2) (видно, что неравенства (3) и (4) получаются из (2) заменой переменных). Перенося все в правую часть, и замечая, что x × cos y + y × cos x – x × cos x + y × cos y = (x – y) × (cos y – cos x), получим, что (2) равносильно (5): (x – y) × (cos y – cos x) ³ 0. (5) Если x £ y, то cos x ³ cos y, так как функция cos x убывает на интервале (0, p/2). Значит, оба сомножителя в (5) неположительны, и неравенство верно. Если же x ³ y, то cos x £ cos y, и, значит, оба сомножителя в (5) неотрицательны. Тем самым доказано, что (5) справедливо для любых чисел x, y из интервала (0, p/2). |
28 Февраля 2004 23:20 Раздел каталога :: Ссылка на задачу
|