358
471
всего разделов:
активных пользователей:
30 мартра 2005
Форумы снова функционируют.
21 декабря 2004
Видимо в связи с обнаруженными дырами в phpBB, форум был взломан, а через него взломано и всё остальное содержимое ceemat.ru. Всё кроме форума восстановлено, ведется дискуссия по поводу его сохранения.
Приносим извинения за неудобства.
29 сентября 2004
Форум обновился до версии 2.0.10
15 мая 2004
Новый раздел: "Программирование"
16 апреля 2004 года
Задачи Ярославского турнира математических боев — 124 задачи с решениями.
29 марта 2004
Таллинская викторина: занимательные вопросы и задачи для увлеченных химией.
Вариант 11 класса (5)
Даны скрещивающиеся прямые l и m. По прямой l перемещается отрезок AB длины a, по прямой m — отрезок CD длины b. Докажите, что объем фигуры ABCD не зависит от места расположения отрезков. |
Высота параллелепипеда h равна расстоянию между плоскостями a и b. Его основания — параллелограмм, длины диагоналей которого равны длинам данных отрезков AB и CD, а угол g между ними — углу между прямыми l и m. Значит, площадь основания равна ½×AB×CD×sin g. Тогда объем параллелепипеда равен ½×h×AB×CD×sin g, то есть не зависит от расположения отрезков AB и CD. Объем треугольной пирамиды ABCD равен 1/3 от объема параллелепипеда, так как получается их него отрезанием четырех пирамид A1ACD, B1BCD, C1CAB, D1DAB, объем каждой из которых равен 1/6 объема всего параллелепипеда. Значит, объем нашей фигуры (как и объем параллелепипеда) не зависит от расположения отрезков AB и CD. |
13 Декабря 2003 14:25 Раздел каталога :: Ссылка на задачу
|
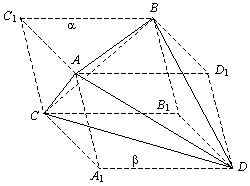Единственным образом можно провести параллельные плоскости a и b,
такие что прямая l лежит в плоскости a, а прямая m — в плоскости b.
Так же единственным образом строится параллелепипед AC1BD1A1CB1D (показано на рисунке),
у которого две противоположные грани лежат в плоскостях a и b.