358
471
всего разделов:
активных пользователей:
30 мартра 2005
Форумы снова функционируют.
21 декабря 2004
Видимо в связи с обнаруженными дырами в phpBB, форум был взломан, а через него взломано и всё остальное содержимое ceemat.ru. Всё кроме форума восстановлено, ведется дискуссия по поводу его сохранения.
Приносим извинения за неудобства.
29 сентября 2004
Форум обновился до версии 2.0.10
15 мая 2004
Новый раздел: "Программирование"
16 апреля 2004 года
Задачи Ярославского турнира математических боев — 124 задачи с решениями.
29 марта 2004
Таллинская викторина: занимательные вопросы и задачи для увлеченных химией.
Вариант 10 класса (5)
Доказать, что четыре расстояния от точки окружности до вершин вписанного в нее квадрата не могут одновременно быть рациональными числами. |
Приравняв правые части равенств, после преобразований получим:
Если бы числа a, b, c и d были рациональными, то рациональным было бы и число
|
13 Декабря 2003 14:20 Раздел каталога :: Ссылка на задачу
|
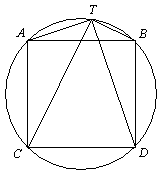Стороны квадрата стягивают дуги по 90° каждая.
Значит, ÐATC = ÐBTD = 45° (показано на рисунке).
Обозначим расстояния от точки T до вершин A, B, C и D квадрата как a, b,
c и d, а сторону квадрата как k. Тогда из треугольников ATC и BTD по теореме косинусов
следуют равенства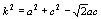
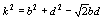
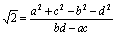
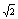, что не так.