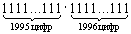358
475
всего разделов:
активных пользователей:
30 мартра 2005
Форумы снова функционируют.
21 декабря 2004
Видимо в связи с обнаруженными дырами в phpBB, форум был взломан, а через него взломано и всё остальное содержимое ceemat.ru. Всё кроме форума восстановлено, ведется дискуссия по поводу его сохранения.
Приносим извинения за неудобства.
29 сентября 2004
Форум обновился до версии 2.0.10
15 мая 2004
Новый раздел: "Программирование"
16 апреля 2004 года
Задачи Ярославского турнира математических боев — 124 задачи с решениями.
29 марта 2004
Таллинская викторина: занимательные вопросы и задачи для увлеченных химией.
Вариант 9 класса (5)
Докажите, что в десятичной записи числа
|
Решение. Данное число — 3990-значное. Предположим, что в его записи каждая цифра встречается менее 400 раз. Тогда число состоит из 399-и единиц, 399-и двоек, …, 399-и девяток и 399-и нулей. Следовательно, сумма его цифр, равная 399×(1 + 2 + … + 9 + 0) = 399 × 45, кратна 9. Значит и само число должно делиться на 9. Но оно раскладывается (по условию) на два множителя, первый из которых не делится на 9, а второй взаимно прост с 3. Противоречие. |
13 Декабря 2003 14:13 Раздел каталога :: Ссылка на задачу
|