358
476
всего разделов:
активных пользователей:
30 мартра 2005
Форумы снова функционируют.
21 декабря 2004
Видимо в связи с обнаруженными дырами в phpBB, форум был взломан, а через него взломано и всё остальное содержимое ceemat.ru. Всё кроме форума восстановлено, ведется дискуссия по поводу его сохранения.
Приносим извинения за неудобства.
29 сентября 2004
Форум обновился до версии 2.0.10
15 мая 2004
Новый раздел: "Программирование"
16 апреля 2004 года
Задачи Ярославского турнира математических боев — 124 задачи с решениями.
29 марта 2004
Таллинская викторина: занимательные вопросы и задачи для увлеченных химией.
Вариант 9 класса (5)
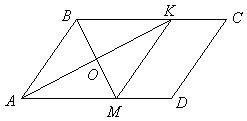
В параллелограмме ABCD стороны AB и BC равны 4 и 7 соответственно. Биссектрисы AK и BM углов параллелограмма пересекаются в точке O (точки K и M лежат на сторонах BC и AD соответственно). Во сколько раз площадь пятиугольника OKCDM больше площади треугольника OAB? |
Решение. Заметим, что ÐBAO + ÐABO = (ÐBAD + ÐABC) : 2 = 90°; отсюда ÐAOB = 90°. Значит треугольник ABK — равнобедренный, AB = BK. Аналогично AB = AM. Таким образом, ABKM — ромб. Он имеет общую высоту с параллелограммом, поэтому SABKM:SABCD = AM : AD = 4 : 7. Значит, SCDMK составляет 3/7 от SABCD, а площадь каждого из треугольников, на которые разбивается ромб диагоналями, — 1/7 от SABCD. Значит, SCDMOK составляет 4/7 от SABCD, откуда SCDMOK : SAOB = 4. |
13 Декабря 2003 14:12 Раздел каталога :: Ссылка на задачу
|
 Ответ: в 4 раза.
Ответ: в 4 раза.