358
471
всего разделов:
активных пользователей:
30 мартра 2005
Форумы снова функционируют.
21 декабря 2004
Видимо в связи с обнаруженными дырами в phpBB, форум был взломан, а через него взломано и всё остальное содержимое ceemat.ru. Всё кроме форума восстановлено, ведется дискуссия по поводу его сохранения.
Приносим извинения за неудобства.
29 сентября 2004
Форум обновился до версии 2.0.10
15 мая 2004
Новый раздел: "Программирование"
16 апреля 2004 года
Задачи Ярославского турнира математических боев — 124 задачи с решениями.
29 марта 2004
Таллинская викторина: занимательные вопросы и задачи для увлеченных химией.
Задачи финальных боев (11)
|
Пусть в белых клетках стоит число a, а в черных — b. Фигурку можно наложить так, чтобы три клетки были черными, а одна — белая, и наоборот, три — белые, а одна — черная. Отсюда следуют равенства: 3b + a = 4, 3a + b = 4. Значит, 3b + a = 3a + b, откуда a = b = 1. |
25 Ноября 2003 20:15 Раздел каталога :: Ссылка на задачу
|
В клетках бесконечной шахматной доски записали числа так, что сумма чисел в любых четырех клетках доски,
составляющих фигуру, показанную на рисунке, равна 4. Докажите, что в каждой клетке стоит число 1.
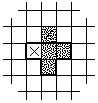Если наложить фигуру так, как показано на рисунке, то видно, что числа, стоящие в клетках, отмеченных
крестиками, должны быть равны. Отсюда следует, что если все клетки раскрасить в шахматном порядке, то в
клетках одного цвета будут стоять равные числа.