Задачи финальных боев (11)

1.

27 августа, когда Саше исполнился 1 год, он нашел мешочек с монетами. Начиная со следующего дня, он стал закидывать их за диван: в первый день — одну монету, во второй — две, в третий — три и так далее. При этом каждый второй день родители вынимали две монеты и возвращали их в мешочек. Когда Саше исполнился 1 год и 1 месяц, он закинул за диван последние монеты, после чего про них все забыли. Сколько монет оказалось под диваном?

2.

Разрезать фигуру, изображенную на рисунке, на 4 равные части.

3.

Найдите пять натуральных чисел, если
a) их произведение — 32, а сумма — 21;
b) их произведение — 420, а сумма — 20.

4.

Сколько существует пятизначных чисел, кратных 3, которые начинаются с цифры 4, а заканчиваются цифрой 2?

5.

“Хорошие числа обладают хорошими свойствами!” — однажды заявил Знайка. “А что хорошего в числе 1000030000300001, которое так хорошо записывается?” — спросил Незнайка. “Это куб натурального числа!” — воскликнул в ответ Знайка. А какого?

6.

На острове проживает 1998 жителей, каждый из которых либо лжец (который всегда врет), либо рыцарь (который всегда говорит правду). Однажды все жители острова разбились на пары, и каждый про своего соседа по паре сказал либо “Он — лжец!”, либо “Он — рыцарь!”. Может ли в итоге получиться поровну как одних фраз, так и других?

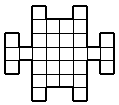
7.

Разрезать фигуру, изображенную на рисунке, на 9 равных частей.

8.

Квадрат натурального числа A + 5 — трехзначное число, а куб числа A – 4 — пятизначное. Найдите A.

9.

Круг разделен 5 прямыми, проходящими через его центр, на 10 секторов. Незнайка хочет расставить в сектора фишки так, чтобы в любых двух полукругах, границами которых являются проведенные прямые, стояло разное количество фишек. Какое минимальное число фишек Незнайка может использовать? (В любой сектор можно ставить несколько фишек или не ставить совсем.)

10.

Сколькими способами в таблице 3 ´  3 можно расставить три единицы, три двойки и три тройки так, чтобы суммы чисел, стоящих в одной строчке или одном столбце, были равны?

11.

В клетках бесконечной шахматной доски записали числа так, что сумма чисел в любых четырех клетках доски, составляющих фигуру, показанную на рисунке, равна 4. Докажите, что в каждой клетке стоит число 1.