Задачи третьего тура боев (14)

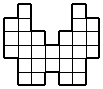
1.

Разрежьте фигуру, изображенную на рисунке, на 4 равные части.

2.

В числе 19981998 Василий заменил все цифры: некоторые увеличил на 1, а остальные — уменьшил на 1, причем равные цифры изменил одинаково. В результате получилось число, кратное 3. Какое?

3.

Трехзначное число A сложили с числом, записанным теми же цифрами, но в обратном порядке. В результате получили четырехзначное число, одинаково читаемое и слева направо и справа налево. Найдите A. Сколько решений имеет задача?

4.

На планете Куб (имеющей форму куба) каждой гранью владеет рыцарь (который всегда говорит правду) или лжец (который всегда врет). Каждый из них утверждает, что большая часть его соседей — лжецы. Сколько рыцарей и сколько лжецов владеют гранями планеты?

5.

Из бумаги склеили куб. По скольким ребрам его можно разрезать, чтобы получить развертку?

6.

Магараджей называется шахматная фигура, которая может бить и как ферзь, и как конь.
a) Сколькими способами можно расположить 4 такие фигуры, не бьющие друг друга, на доске 5 ´ 5?
b) Можно ли на доске 6 ´ 6 расположить пять таких фигур, не бьющих друг друга?

7.

В автобусе имеются одноместные и двухместные сидения. Кондуктор заметил, что когда в автобусе сидело 13 человек, то 9 сидений оказалось полностью свободными. В следующий раз сидели 10 человек, а свободных сидений осталось 6. Сколько сидений в автобусе?

8.

На доске написали числа 1, 2, 3, …, 98. Одно число изменили на 1, потом одно из написанных изменили на 2, затем — на 3, и так далее. Можно ли таким образом получить другие 98 подряд идущих натуральных чисел?

9.

На столе стоит пять коробок. В первой — одна бусинка, во второй — две, …, в пятой — пять. Первым ходом можно положить в любую коробку или вытащить из нее 1 бусинку, вторым — положить или вытащить 2 бусинки (из той же или другой коробки), третьим — 3, и так далее. Можно ли за несколько ходов сделать так, чтобы в первой коробке было 98 бусинок, во второй — 99, …, в пятой — 102?

10.

Существует ли кратное 7 натуральное десятизначное число, все цифры которого различны?

11.

На прямой отметили несколько точек. После этого между любыми двумя соседними точками поставили по точке. Такую операцию повторили 3 раза. В результате на прямой оказалось ровно 65 точек. Сколько точек было на прямой первоначально?

12.

Класс, в котором 36 школьников, построили в виде квадрата, в котором 6 рядов и 6 шеренг. Если в каждой шеренге выбрать самого высокого, то самым низким из них будет Игорь. Если
a) в каждой шеренге;
b) в каждом ряду
выбрать самого низкого, то самым высоким из них будет Юра. Может ли Юра быть выше Игоря?

13.

Кузнечик живет на координатной прямой. Каждый день длина первого прыжка кузнечика равна 1, длина второго — 2, третьего — 4, и так далее (каждый раз длина прыжка увеличивается в 2 раза). Может ли кузнечик в течение одного дня побывать дважды в одной точке?

14.

В банку поместили несколько бактерий. Оказалось, что в течение каждой из следующих 9 секунд ровно половина всех имеющихся бактерий делилась пополам. Докажите, что в начале в банке было, по крайней мере, 500 бактерий.