358
476
всего разделов:
активных пользователей:
30 мартра 2005
Форумы снова функционируют.
21 декабря 2004
Видимо в связи с обнаруженными дырами в phpBB, форум был взломан, а через него взломано и всё остальное содержимое ceemat.ru. Всё кроме форума восстановлено, ведется дискуссия по поводу его сохранения.
Приносим извинения за неудобства.
29 сентября 2004
Форум обновился до версии 2.0.10
15 мая 2004
Новый раздел: "Программирование"
16 апреля 2004 года
Задачи Ярославского турнира математических боев — 124 задачи с решениями.
29 марта 2004
Таллинская викторина: занимательные вопросы и задачи для увлеченных химией.
Задачи первого тура боев (11)
Можно ли расставить по кругу
|
Ответ: нельзя.
a ± 6 ± 6 ± 6 ± 6 ± 6 = a. Это равенство не может выполняться ни при одной комбинации знаков, потому что количества плюсов и минусов будут разными (так как всего их — нечетное число).
a ± 1 ± 1 ± … ± 1 = a (всего число 1 прибавляется или вычитается 99 раз). Это равенство также не может выполняться ни при одной комбинации знаков. c) Исходя из решения предыдущих пунктов, достаточно доказать, что если соединить отрезками пары чисел, между которыми стоит ровно 4 числа, то получиться цикл, состоящий из всех 99 чисел. Переходя от одного числа по отрезку до другого, мы передвигаемся “на 5 чисел”. Если через n таких передвижений мы вернемся к первоначальному числу, сделав m кругов, то передвинемся, с одной стороны, на 5n чисел, с другой стороны, на 99m. То есть, 5n = 99m. Так как 5 и 99 — взаимно простые числа, то наименьшее n равно 99. Значит, все 99 чисел в цикле будут. |
25 Ноября 2003 19:34 Раздел каталога :: Ссылка на задачу
|
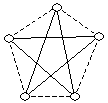 a) Для каждого числа есть только два числа, не соседних с ним (рисунок 16). Если соединить несоседние числа
отрезками, то получиться цикл, в котором 5 ребер. Тогда, если одно из чисел a, то следующее в цикле
— a ± 6, следующее —
(a ± 6) ± 6, и так далее.
Вернувшись к первому числу, получим, что
a) Для каждого числа есть только два числа, не соседних с ним (рисунок 16). Если соединить несоседние числа
отрезками, то получиться цикл, в котором 5 ребер. Тогда, если одно из чисел a, то следующее в цикле
— a ± 6, следующее —
(a ± 6) ± 6, и так далее.
Вернувшись к первому числу, получим, что
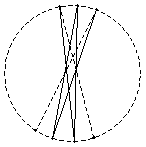 b) Два числа, между каждым из которых и данным стоит ровно 48 чисел, являются соседними. Если соединить
отрезками пары чисел так же, как и в пункте a), то получиться цикл соединяющий все числа (это следует
из построения; показано на рисунке справа). В цикле 99 чисел. Повторим рассуждения решения пункта a):
если одно из чисел a, то следующее в цикле — a ± 1,
следующее — (a ± 1) ± 1,
и так далее; вернувшись к первому числу, получим, что
b) Два числа, между каждым из которых и данным стоит ровно 48 чисел, являются соседними. Если соединить
отрезками пары чисел так же, как и в пункте a), то получиться цикл соединяющий все числа (это следует
из построения; показано на рисунке справа). В цикле 99 чисел. Повторим рассуждения решения пункта a):
если одно из чисел a, то следующее в цикле — a ± 1,
следующее — (a ± 1) ± 1,
и так далее; вернувшись к первому числу, получим, что