358
471
всего разделов:
активных пользователей:
30 мартра 2005
Форумы снова функционируют.
21 декабря 2004
Видимо в связи с обнаруженными дырами в phpBB, форум был взломан, а через него взломано и всё остальное содержимое ceemat.ru. Всё кроме форума восстановлено, ведется дискуссия по поводу его сохранения.
Приносим извинения за неудобства.
29 сентября 2004
Форум обновился до версии 2.0.10
15 мая 2004
Новый раздел: "Программирование"
16 апреля 2004 года
Задачи Ярославского турнира математических боев — 124 задачи с решениями.
29 марта 2004
Таллинская викторина: занимательные вопросы и задачи для увлеченных химией.
Четвертый тур боев (8)
Внутри треугольника отмечены середины медиан. Докажите, что сумма расстояний от отмеченных точек до сторон треугольника меньше периметра треугольника. |
Длина перпендикуляра MC2, опущенного на сторону AB треугольника не более MC1 (так как MC2 — гипотенуза прямоугольного треугольника MC1C2). Аналогично, длина перпендикуляра MA2, опущенного на сторону BC треугольника не более MA1. То есть, сумма расстояний от точки M до сторон AB и BC не более средней линии A1C1. Значит, не более AB1. Длина перпендикуляра MB2, опущенного на сторону AC треугольника, равна расстоянию от средней линии A1C1 до стороны AC, то есть половине треугольника высоты, опущенной на сторону AC, длина которой не более стороны AB. Тогда, длина MB2 не более AC1 — половины стороны AB. Значит, сумма расстояний от точки M до сторон треугольника не более AC1 + AB1. Аналогично, сумма расстояний от середин медиан AA1 и CC1 до сторон треугольника не более соответственно A1C + B1C и A1B + C 1B. Поэтому, сумма расстояний от отмеченных точек до сторон треугольника меньше периметра треугольника. |
21 Ноября 2003 15:49 Раздел каталога :: Ссылка на задачу
|
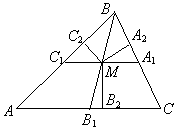Середины медиан треугольника лежат на средних линиях. Рассмотрим точку M — середину медианы
BB1 треугольника ABC (смотри рисунок). Она лежит на средней линии
A1C1.