358
476
всего разделов:
активных пользователей:
30 мартра 2005
Форумы снова функционируют.
21 декабря 2004
Видимо в связи с обнаруженными дырами в phpBB, форум был взломан, а через него взломано и всё остальное содержимое ceemat.ru. Всё кроме форума восстановлено, ведется дискуссия по поводу его сохранения.
Приносим извинения за неудобства.
29 сентября 2004
Форум обновился до версии 2.0.10
15 мая 2004
Новый раздел: "Программирование"
16 апреля 2004 года
Задачи Ярославского турнира математических боев — 124 задачи с решениями.
29 марта 2004
Таллинская викторина: занимательные вопросы и задачи для увлеченных химией.
Третий тур боев (14)
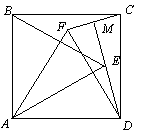
Внутри (вне) квадрата ABCD взяты точки E и F такие, что треугольники AEB и AFD
— равносторонние.
|
a) Из равенства треугольников AED и DFC следует равенство углов EDA и FCD, откуда ÐEDC = ÐBCF; ÐEDC + ÐEDA = 90°, тогда, ÐEDC + ÐDCF = 90°, то есть ÐDMC — прямой.
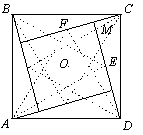
b) Решение первое. Если построить правильные треугольники на сторонах квадрата AB, BC, CD и AD, и соединить их вершины, не совпадающие с вершинами квадрата, соответственно с вершинами D, A, B, C квадрата, то полученные прямые (смотри рисунок) ограничат квадрат, сторонами которого будут прямые ED и FC, а центром — точка O, являющаяся центром квадрата ABCD. Поэтому, точка O равноудалена от прямых ED и FC.
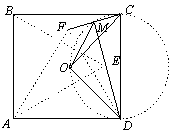
Решение второе. Так как Ð CMD =Ð COD = 90° , то точки C, D, O, M лежат на одной окружности. Тогда, ÐOMD =ÐOCD = 45°. То есть угол ÐOMD равен половине прямого угла FMD. Значит, OM — биссектриса угла FMD, поэтому точка O равноудалена от прямых ED и FC.
|
Замечание. Данные доказательства подходят как для случая, когда треугольники лежат вне квадрата, так и для случая, когда треугольники внутри. |
21 Ноября 2003 15:22 Раздел каталога :: Ссылка на задачу
|