358
471
всего разделов:
активных пользователей:
30 мартра 2005
Форумы снова функционируют.
21 декабря 2004
Видимо в связи с обнаруженными дырами в phpBB, форум был взломан, а через него взломано и всё остальное содержимое ceemat.ru. Всё кроме форума восстановлено, ведется дискуссия по поводу его сохранения.
Приносим извинения за неудобства.
29 сентября 2004
Форум обновился до версии 2.0.10
15 мая 2004
Новый раздел: "Программирование"
16 апреля 2004 года
Задачи Ярославского турнира математических боев — 124 задачи с решениями.
29 марта 2004
Таллинская викторина: занимательные вопросы и задачи для увлеченных химией.
Второй тур боев (10)
Докажите, что если в четырехугольники отрезки, соединяющие середины противоположных сторон перпендикулярны, то его диагонали равны. |
Пусть A1, B1, C1, D1 — середины сторон AB, BC, CD, AD четырехугольника ABCD соответственно. Лемма. A1B1C1D1 — параллелограмм.
В параллелограмме A1B1C1D1 диагонали перпендикулярны, значит, он является ромбом. Тогда, A1B1 = B1C1. Отрезки A1B1 и B1C1 — средние линии треугольников ABС и CBD с основаниями AC и BD. Значит, AC = BD. |
21 Ноября 2003 14:51 Раздел каталога :: Ссылка на задачу
|
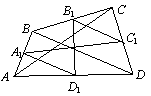Доказательство леммы. Действительно, A1D1 и
B1C1 — средние линии треугольников ABD и CBD с
общим основанием BD (смотри рисунок), тогда
A1D1 = 1/2×BD = B1C1
и A1D1 ½½ BD ½½ B1C1,
откуда следует утверждение леммы.