358
476
всего разделов:
активных пользователей:
30 мартра 2005
Форумы снова функционируют.
21 декабря 2004
Видимо в связи с обнаруженными дырами в phpBB, форум был взломан, а через него взломано и всё остальное содержимое ceemat.ru. Всё кроме форума восстановлено, ведется дискуссия по поводу его сохранения.
Приносим извинения за неудобства.
29 сентября 2004
Форум обновился до версии 2.0.10
15 мая 2004
Новый раздел: "Программирование"
16 апреля 2004 года
Задачи Ярославского турнира математических боев — 124 задачи с решениями.
29 марта 2004
Таллинская викторина: занимательные вопросы и задачи для увлеченных химией.
Второй тур боев (10)
Какое наименьшее число фишек нужно расставить
|
На доске 8 ´ 8 можно отметить 16 непересекающихся прямых, на каждой из которых должна находиться хотя бы одна фишка. То есть менее, чем 16 фишками не обойтись. Если фишки поставить в 16 клеток, отмеченных серым цветом, то получится требуемая расстановка.
На доске 9 ´ 9 можно также отметить 16 непересекающихся прямых (рисунок внизу). Но чтобы “выбить” клетки, отмеченные точками, необходимо не менее 3 фишек. Поэтому, наименьшее количество фишек равно 19 (их можно расставить в клетки, отмеченные серым цветом). |
21 Ноября 2003 14:44 Раздел каталога :: Ссылка на задачу
|
 a) Ответ: 16.
a) Ответ: 16.
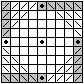 b) Ответ: 19.
b) Ответ: 19.