358
471
всего разделов:
активных пользователей:
30 мартра 2005
Форумы снова функционируют.
21 декабря 2004
Видимо в связи с обнаруженными дырами в phpBB, форум был взломан, а через него взломано и всё остальное содержимое ceemat.ru. Всё кроме форума восстановлено, ведется дискуссия по поводу его сохранения.
Приносим извинения за неудобства.
29 сентября 2004
Форум обновился до версии 2.0.10
15 мая 2004
Новый раздел: "Программирование"
16 апреля 2004 года
Задачи Ярославского турнира математических боев — 124 задачи с решениями.
29 марта 2004
Таллинская викторина: занимательные вопросы и задачи для увлеченных химией.
Первый тур боев (12)
a) В параллелограмме ABCD биссектриса угла A проходит через середину стороны BC. Докажите, что биссектриса угла D также проходит через середину BC. b) В параллелограмме ABCD биссектриса угла A проходит через точку E на стороне BC, а биссектриса угла D через точке F стороны BC. Найти длину отрезка EF, если стороны AB и BC параллелограмма равны соответственно a и b. |
Тогда CD = AB = BE = EC, откуда треугольник ECD также равнобедренный. Получаем, что ÐCED = ÐCDE. Но ÐCED = ÐEDA. То есть ÐCDE = ÐEDA, откуда следует, что DE — биссектриса угла CDA.
Из результатов задачи пункта a) следует, что BE = CF = AB = a. Тогда, EF = 2a – b. Однако, если рассмотреть случай, когда биссектрисы AE и DF пересекаются вне параллелограмма, то EF = b – 2a; в общем случае EF = ½b – 2a½. |
21 Ноября 2003 14:27 Раздел каталога :: Ссылка на задачу
|
a) Пусть точка E — середина BC.
Из равенств углов ÐBAE = ÐEAD
(так как AE — биссектриса угла BAD), ÐEAD = ÐBEA
(так как прямые AD и BC параллельны) следует, что треугольник ABE равнобедренный,
то есть AB = BE.
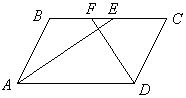b) Ответ: ½b – 2a½.