358
471
всего разделов:
активных пользователей:
30 мартра 2005
Форумы снова функционируют.
21 декабря 2004
Видимо в связи с обнаруженными дырами в phpBB, форум был взломан, а через него взломано и всё остальное содержимое ceemat.ru. Всё кроме форума восстановлено, ведется дискуссия по поводу его сохранения.
Приносим извинения за неудобства.
29 сентября 2004
Форум обновился до версии 2.0.10
15 мая 2004
Новый раздел: "Программирование"
16 апреля 2004 года
Задачи Ярославского турнира математических боев — 124 задачи с решениями.
29 марта 2004
Таллинская викторина: занимательные вопросы и задачи для увлеченных химией.
Финальный тур боев (13)
Каждая из клеток квадрата 5 ´ 5 покрашена в один из четырех цветов так, что в любом квадрате 2 ´ 2 встречаются все 4 цвета. Какое наибольшее число клеток при этом может быть окрашено в один цвет? |
Ответ: 9.
|
16 Ноября 2003 12:53 Раздел каталога :: Ссылка на задачу
|
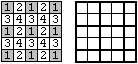Разделим доску на 9 частей так, как показано на правом рисунке.
В каждой части не может две клетки быть окрашенными в один цвет, иначе в каком-то квадрате
2 ´ 2 найдутся две клетки одного цвета. То есть более 9 клеток
одного цвета быть не может. На левом рисунке показано, как раскрасить клетки так, чтобы нашлось 9 клеток
одного цвета.